Pelajaran Matematika Perbandingan Dan Skala

Bimbel Jakarta Timur | Bimbel Diah Jakarta Timur | WA : +6285875969990


Merupakan sebagai salah satu materi yang diujikan dalam Ujian Sekolah Berstandar Nasional untuk tingkat Sekolah Dasar. Salah satu indikator soalnya adalah siswa dapat menyelesaikan soal cerita sederhana yang berkaitan dengan skala atau perbandingan lainnya.

Perbandingan adalah membandingkan dua nilai atau lebih dari suatu besaran yang sejenis dan dinyatakan dengan cara yang sederhana.

Skala adalah perbandingan antara jarak pada gambar dengan jarak yang sebenarnya. 

Selanjutnya : Perbandingan Dan Skala (Materi Sekolah Dasar)

Tag:

materi perbandingan dan skala kelas 5 sd pdf

materi perbandingan dan skala kelas 5 sd

soal perbandingan dan skala

rumus perbandingan dan skala

soal perbandingan dan skala kelas 5

hubungan perbandingan dan skala

materi perbandingan dan skala kelas 5 sd ppt

makalah perbandingan dan skala






 

on Sunday, August 20, 2017 | , , | A comment?

Pelajaran Matematika Bangun Datar

segitiga

Bangun datar adalah kelompok bangun-bangun dua dimensi seperti segitiga, persegi, belah ketupat, jajaran genjang, layangan, trapesium, lingkaran

Setiap bangun memiliki sifat-sifat dan rumus luas serta rumus kelilingnya. Berikut adalah soal-soal latihan beserta pembahasan tentang luas dan keliling bangun datar yang dipelajari di sekolah dasar. 

Bentuk 2D (dua dimensi) adalah bangun datar yang hanya memiliki dua dimensi – panjang dan lebar, tanpa ketebalan atau kedalaman. Misalnya, selembar kertas berbentuk dua dimensi. Ini terdiri dari panjang dan lebar tetapi tidak memiliki kedalaman atau tinggi. Beberapa bentuk 2D yang umum adalah persegi, persegi panjang, segitiga, lingkaran, dan segi enam. Dibandingkan dengan ini, bentuk 3D (tiga dimensi) memiliki tiga dimensi – panjang, lebar, dan tinggi. Misalnya, dadu adalah tiga dimensi karena terdiri dari panjang, lebar, dan tinggi. Beberapa bentuk 3D yang umum adalah kuboid, kerucut, piramida, dan silinder. Mari kita pelajari lebih lanjut tentang bentuk 2D di artikel ini.

Dalam geometri, bangun datar dapat didefinisikan sebagai bangun datar yang benar-benar datar dan hanya memiliki dua dimensi – panjang dan lebar. Mereka tidak memiliki ketebalan apapun dan hanya dapat diukur dengan dua dimensi. Poligon adalah bangun datar yang terdiri dari segmen garis lurus yang dihubungkan satu sama lain, sehingga memberikan bentuk tertutup. Lingkaran, persegi, persegi panjang, dan segitiga adalah beberapa contoh benda dua dimensi dan bentuk-bentuk ini dapat digambar di atas kertas. Semua bentuk 2-D memiliki sisi, simpul (sudut), dan sudut internal, kecuali lingkaran, yang merupakan sosok melengkung. Bangun datar dengan setidaknya tiga sisi lurus disebut poligon dan itu termasuk segitiga, bujur sangkar, dan segi empat.

Bangun datar dapat diklasifikasikan sebagai beraturan atau tidak beraturan berdasarkan panjang dan sudut interiornya:

Suatu bangun datar dikatakan beraturan jika semua sisinya sama panjang dan semua sudut dalamnya sama besar.

Suatu bangun datar tidak beraturan jika semua sisinya tidak sama panjang dan semua sudutnya tidak sama besar.

Selanjutnya : 

Soal-soal Bangun Datar (Materi Sekolah Dasar)


Bangun datar adalah bangun dua dimensi yang dibatasi oleh garis-garis lurus atau garis lengkung. Bangun datar memiliki keliling dan luas. Bangun datar yang dibahas untuk materi sekolah dasar diantaranya adalah segitiga, persegi, persegi panjang, jajar genjang, trapesium, belah ketupat, layang-layang dan lingkaran. Bangun datar-bangun datar tersebut dapat dibentuk menjadi gabungan bangun datar.  Berikut adalah : 

soal dan pembahasan bangun datar gabungan



Tag:

gambar bangun datar

rumus bangun datar

nama dan gambar bangun datar

keliling bangun datar

bentuk bangun datar

bangun datar segitiga

luas bangun datar

bangun datar persegi

luas dan keliling bangun datar gabungan

contoh soal luas dan keliling bangun datar gabungan dan jawabannya

luas bangun datar gabungan

bangun datar gabungan dan alasannya

keliling bangun datar gabungan persegi panjang dan setengah lingkaran

contoh soal luas bangun datar gabungan

cara menghitung luas bangun datar gabungan persegi dan persegi panjang

jika luas bangun datar pada gambar b yaitu 84 cm keliling bangun datar gabungan

soal gabungan bangun datar kelas 6 sd

contoh soal bangun datar gabungan dan jawabannya kelas 6

contoh soal luas dan keliling bangun datar gabungan dan jawabannya

soal keliling bangun datar gabungan

contoh soal bangun datar gabungan persegi panjang dan lingkaran

soal cerita gabungan lingkaran dan bangun datar

contoh soal luas dan keliling bangun datar dan jawabannya

keliling dari gabungan dua persegi pada gambar adalah






 

on Thursday, August 3, 2017 | , , | A comment?

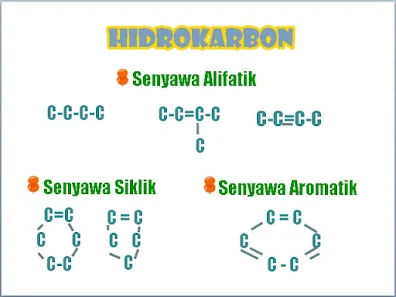
Pelajaran IPA Kimia HIDROKARBON

Hidro Karbon
Senyawa hidrokarbon terdiri dari atom karbon (C) dan atom hidrogen (H). Atom C dan H dalam senyawa dapat ditunjukkan dengan uji pembakaran. Pada pembakaran sempurna, atom C akan menjadi CO2 sedangkan atom H akan menjadi H2O.


Atom karbon mempunyai 4 elektron valensi sehingga atom C dapat membentuk empat ikatan kovalen untuk mencapai konfigurasi oktet. Atom karbon juga memiliki kemampuan membentuk rantai. Rantai karbon dapat berbentuk lurus, bercabang ataupun melingkar.

Berdasarkan bentuk rantainya, senyawa karbon dapat dibagi menjadi senyawa alifatik, senyawa siklik dan senyawa aromatik.


Senyawa Alifatik : Senyawa hidrokarbon dengan rantai terbuka  jenuh (ikatan tunggal) maupun tidak jenuh (ikatan rangkap).

Senyawa Siklik : Senyawa hidrokarbon yang rantai karbonnya tertutup atau melingkar.

Senyawa Aromatik  : Senyawa hidrokarbon siklik yang mempunyai ikatan-ikatan karbon tunggal dan rangkap selang seling. 


Senyawa hidrokarbon alifatik terdiri dari alkana, alkena dan alkuna.

Selanjutnya : HIDROKARBON

Tag :


materi hidrokarbon
senyawa hidrokarbon
sumber hidrokarbon
jenis hidrokarbon
contoh senyawa hidrokarbon dalam kehidupan sehari-hari
rumus senyawa hidrokarbon
hidrokarbon alifatik
hidrokarbon adalah sebuah senyawa yang terdiri dari

 

on Sunday, July 30, 2017 | , , , | A comment?

Hubungan Satuan Waktu, Panjang, Berat dan Kuantitas


Hubungan Satuan Waktu

Dalam ilmu pasti, terutama matematika kita perlu tahu konversi (hubungan antar satuan). Sebenarnya di dunia kita akan menjumpai banyak ragam satuan yang dipakai di suatu negara atau suatu daerah. Akan tetapi ada satuan yang dipakai umum atau sebagai standar yang disebut satuan baku. Berikut adalah beberapa satuan baku yang kita pelajari untuk tingkatan Sekolah Dasar.

Yang akan kita bahas disini adalah :

A. Satuan Waktu
B. Satuan Panjang 
C. Satuan Luas
D. Satuan Volume
E. Satuan Berat
F. Satuan Kuantitas


Kemudian Coba Juga soal-soal latihan berikut : 




Tag:

hubungan antar satuan berat
hubungan antar satuan kuantitas
hubungan antar satuan panjang
satuan kuantitas berat
satuan kuantitas lengkap
soal satuan kuantitas
satuan panjang dan berat
makalah satuan panjang dan berat


 

on Saturday, July 22, 2017 | , , | A comment?

Menghitung Luas Segi-n Beraturan Dengan Trigonometri

Bimbel Jakarta Timur | Bimbel DIah Jakarta Timur | WA : +6285875969990

Segi-n beraturan yaitu bangun datar atau bentuk dimensi 2 yang terdiri dari garis-garis bersambungan membentuk bangun tertutup dengan  sisi yang sama panjang dan  sudut yang sama besar. 
Segi-n beraturan  adalah poligon jenis khusus. Ini adalah poligon yang sama sisi (semua sisi kongruen) dan sama sudut (semua sudut internal kongruen). Kuadrat adalah teratur. Persegi panjang bukan karena tidak sama sisi. Belah ketupat tidak teratur karena tidak bersudut sama.

Sebuah poligon biasa, ingat, adalah poligon yang sisi dan sudut interior semua kongruen.

Sebuah poligon bersisi n beraturan memiliki simetri putar orde n.

Semua simpul dari Segi-n beraturan  terletak pada lingkaran yang sama (lingkaran terbatas); yaitu, mereka adalah titik konsiklik. Artinya, Segi-n beraturan adalah poligon siklik.

Bersama-sama dengan sifat sisi-sisi yang sama panjang, ini menyiratkan bahwa setiap Segi-n beraturan  juga memiliki lingkaran bertulisan atau lingkaran yang bersinggungan dengan setiap sisi di titik tengahnya. Jadi Segi-n beraturan  adalah poligon tangensial.

Pusat Segi-n beraturan  adalah titik di mana semua simpul berjarak sama. Jari-jari Segi-n beraturan  adalah segmen dengan satu titik akhir di pusat dan titik akhir lainnya di salah satu simpul. Jadi, ada n jari-jari dalam Segi-n beraturan  bersisi n. Pusat dan jari-jari Segi-n beraturan  sama dengan pusat dan jari-jari lingkaran yang dibatasi oleh Segi-n beraturan  tersebut.

Apotema Segi-n beraturan  adalah segmen dengan satu titik ujung di tengah dan titik akhir lainnya di titik tengah salah satu sisinya. Apotema Segi-n beraturan  adalah garis bagi tegak lurus dari sisi mana pun yang memiliki titik ujungnya. Sudut pusat Segi-n beraturan  adalah sudut yang titik sudutnya merupakan pusat dan sinar-sinarnya, atau sisi-sisinya, mengandung titik-titik ujung dari sisi Segi-n beraturan . Jadi, sebuah Segi-n beraturan  bersisi n memiliki n apotema dan n sudut pusat, yang masing-masing berukuran 360/n derajat. Setiap apotema adalah garis bagi sudut dari sudut pusat yang memuat sisi tempat apotema tersebut memanjang.

Apa itu Luas Poligon?
Dalam geometri, luas didefinisikan sebagai daerah yang ditempati di dalam batas bangun datar dua dimensi. Oleh karena itu, luas poligon adalah total ruang atau wilayah yang dibatasi oleh sisi-sisi poligon.

Bagaimana Cara Mencari Luas Poligon?
Poligon biasa seperti persegi panjang, bujur sangkar, trapesium, jajaran genjang, dll., Memiliki rumus yang telah ditentukan sebelumnya untuk menghitung luasnya.

Namun, untuk Segi-n beraturan , luasnya dihitung dengan membagi Segi-n beraturan  menjadi bagian-bagian kecil dari Segi-n beraturan 

Luas Segi-n beraturan 
Menghitung luas Segi-n beraturan  bisa sesederhana mencari luas segitiga beraturan. Segi-n beraturan  memiliki panjang sisi yang sama dan besar sudut yang sama besar

Selanjutnya Gambar-gambar, rumus-rumus dan cara menghitung : Menghitung Luas Segi-n Beraturan Dengan Trigonometri


Tag:

contoh soal luas segi n beraturan
contoh soal luas segi n beraturan kelas 10
luas segi-n beraturan jika diketahui sisinya
rumus keliling segi-n beraturan
contoh segi-n beraturan
sifat-sifat segi-n beraturan
luas segitiga
rumus keliling segi 12














 

on Friday, May 5, 2017 | , , | A comment?

Aturan Sinus, Cosinus dan Luas Segitiga

 

Hukum Sinus (aturan sinus) adalah aturan penting yang berkaitan dengan sisi dan sudut segitiga apa pun (tidak harus siku-siku!), Luas segitiga sembarang adalah 1/2 absinC 



Cara menentukan aturan mana yang akan digunakan:

  1. Aturan luas: jika tidak ada tinggi tegak lurus yang tersedia.
  2. Aturan sinus: jika tidak ada sudut siku-siku yang tersedia. dua sisi dan sebuah sudut tersedia (tidak termasuk sudut) dan dua sudut dan satu sisi tersedia.
  3. Aturan cosinus: jika tidak ada sudut siku-siku yang tersedia dan jika dua sisi yang termasuk sudut 


Selanjutnya (Keterangan Pembahasan, Rumus, dan soal-soal) : 

Aturan Sinus, Cosinus dan Luas Segitiga

Soal-soal Aturan Sinus dan Aturan Cosinus


Tag :


lks aturan sinus, cosinus dan luas segitiga

soal aturan sinus cosinus dan luas segitiga

luas segitiga aturan sinus

aturan sinus, cosinus dan luas segitiga pdf

contoh soal aturan sinus dan cosinus beserta jawabannya

luas segitiga aturan cosinus

rumus aturan sinus

aturan luas segitiga dalam trigonometri




 

on Friday, April 28, 2017 | , , | A comment?
Newer entries
Older entries