Volume dan Luas Permukaan Bangun Ruang Gabungan
Bangun Ruang Gabungan yaitu dua atau lebih bangun ruang yang digabung dengan bertumpuk berlekatan atau berada dalam salah satu bangun ruang tertentu. Adapun yang akan kita bahas pada tulisan ini adalah bangun ruang yang bertumpuk ataupun berlekatan.
Bangun Ruang adalah bangun yang terdiri dari padatan geometris umum. Padatan yang terdiri dari umumnya prisma, piramida, kerucut, silinder dan bola. Untuk menemukan luas permukaan dan volume gabungan padatan, kita perlu mengetahui cara menemukan luas permukaan dan volume prisma, piramida, kerucut, silinder, dan bola.
Luas permukaan total dari Bangun Ruang Gabungan yaitu jumlah dari total luas permukaan dari masing-masing dari bangun ruang gabungan, tidak termasuk bagian yang tumpang tindih dari setiap gambar. Sedangkan volume padatan gabungan adalah jumlah volume dari masing-masing padatan yang membentuk padatan gabungan.
Volume bangun ruang gabungan adalah jumlah volume dari bangun ruang-bangun ruang yang tergabung dalam soal yang dimaksud. Jadi, untuk mencari volume gabungannya, kamu hanya perlu menghitung volume masing-masing bangun lalu menjumlahkannya.
Volume gabungan = Volume I + Volume II + Volume III + ...
untuk menghitung luas permukaan bangun ruang gabungan dapat dihitung dengan rumus berikut :
Luas Permukaan Gabungan =
Luas permukaan I + Luas permukaan II - (2 x luas bidang himpit)
untuk melanjutkan ke soal dan pembahasan selengkapnya klik dibawah ini:
Volume dan Luas Permukaan Bangun Ruang Gabungan (Materi SD)
Tag:
soal luas permukaan bangun ruang gabungan kelas 6
hitunglah luas permukaan bangun 3
luas permukaan bangun ruang kubus
volume bangun gabungan kubus dan balok di samping adalah
rumus luas permukaan bangun ruang gabungan balok dan kubus
soal bangun ruang gabungan
soal hots luas permukaan bangun ruang
luas permukaan bangun ruang gabungan di atas adalah
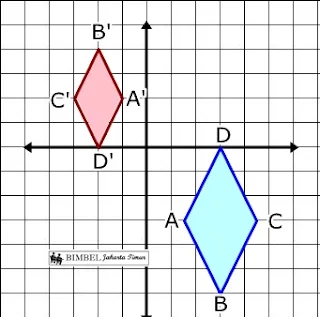
Pelajaran Matematika Transformasi Geometri
Transformasi artinya mengubah. Oleh karena itu, transformasi geometris berarti membuat beberapa perubahan dalam bentuk geometris tertentu.
Menghubungkan Konsep Geometris dan Aljabar
Transformasi adalah istilah umum untuk empat cara khusus untuk memanipulasi bentuk dan/atau posisi titik, garis, atau bangun geometris. Bentuk asli dari objek disebut Pra-Gambar dan bentuk akhir dan posisi objek adalah Gambar di bawah transformasi.
Ada empat jenis transformasi dalam Matematika:
Cerminan
Dalam refleksi, setiap titik berjarak sama dari garis tetap. Garis ini kadang-kadang disebut garis simetri. Dalam refleksi, Gambar berukuran sama dengan Pra-Gambar.
Rotasi
"Rotasi" berarti berputar di sekitar pusat.
Jarak dari pusat ke setiap titik pada bentuk tetap sama. Setiap titik membuat lingkaran di sekitar pusat. Dalam rotasi, Pra-Gambar dan Gambar berukuran sama.
Translasi
"Translasi" secara sederhana berarti bergerak. Dalam translasi, setiap titik pada bangun harus bergerak dengan jarak dan arah yang sama. Dalam terjemahan, ukuran Gambar adalah ukuran yang sama dengan Pra-Gambar.
Dilatasi
"Dilatasi" berarti mengubah ukuran. Namun, ketika Anda mengubah ukuran bentuk, bentuknya menjadi lebih besar atau lebih kecil, namun tetap terlihat serupa. Artinya, semua sudut adalah sama dan sisi-sisinya sebanding. Dalam dilatasi, ukuran Gambar dan Pra-Gambar berbeda. Dilatasi juga disebut kompresi, pembesaran atau kontraksi.
Transformasi yang mempertahankan kongruensi disebut isometri. Dengan kata lain, transformasi di mana Gambar dan Pra-Gambar memiliki panjang sisi dan ukuran sudut yang sama. Translasi, refleksi, dan rotasi adalah isometri. Translasi dianggap sebagai "isometri langsung" karena tidak hanya mempertahankan keselarasan, tetapi juga, tidak seperti refleksi dan rotasi, mempertahankan orientasinya.
Di sisi lain, dilatasi bukan isometri karena Bayangannya tidak kongruen dengan Pra Bayangannya.
Komposisi transformasi berarti bahwa dua atau lebih transformasi akan dilakukan pada satu objek. Misalnya, kita bisa melakukan refleksi dan kemudian terjemahan pada titik yang sama.
Koneksi ke Fungsi Aljabar
Transformasi fungsi mengambil apa pun yang merupakan fungsi dasar f(x) dan kemudian "mengubah" fungsi tersebut dengan cara tertentu. Transformasi fungsi dapat dilakukan dengan memanipulasi fungsi dengan operasi (penambahan, pengurangan, perkalian atau pembagian). Dengan mengubah fungsi, grafik fungsi dapat dipindahkan atau "diubah".
Mari kita gunakan fungsinya, f(x) = x^3
Jika kita mengubah f(x) dengan menambahkan nilai konstan, kita mengubah grafik. Perhatikan grafik g(x) = x^3+ 3. Grafik g(x) “diterjemahkan” naik 3 satuan dari f(x). Karena merupakan translasi, maka bentuk dan ukuran graf g(x) sama dengan f(x). Terjemahan aljabar mengikuti aturan yang sama dengan terjemahan geometris.
Berikut ini adalah tentang Soal Transformasi Geometri berikut jawaban dan pembahasannya agar mudah dipelajari
Soal Transformasi Geometri Kelas 9
Tag:
transformasi geometri kelas 11
soal transformasi geometri kelas 11
contoh soal transformasi geometri
materi transformasi geometri
transformasi geometri yang merubah ukuran adalah
transformasi geometri kelas 12
rumus transformasi geometri
transformasi geometri kelas 9
Pelajaran IPA Fisika Gerak Parabola
Gerak parabola yaitu gerak yang lintasannya bentuk parabola. Gerak parabola ini perpaduan gerak lurus beraturan (GLB) pada sumbu horisontal dan gerak lurus berubah beraturan (GLBB) pada sumbu vertikal. Percepatan yang berpengaruh pada sumbu vertikal adalah percepatan gravitasi.
Gerak Parabola adalah gerak suatu benda yang dilempar atau diproyeksikan ke udara, hanya dikenai percepatan gravitasi. Objek itu disebut Parabola, dan lintasannya disebut lintasannya. Gerak benda jatuh, seperti yang tercakup dalam Dasar-dasar Pemecahan Masalah untuk Kinematika Satu Dimensi, adalah jenis gerak Parabola satu dimensi sederhana di mana tidak ada gerakan horizontal. Pada bagian ini, kita mempertimbangkan gerakan Parabola dua dimensi, seperti sepak bola atau benda lain yang hambatan udaranya dapat diabaikan.
Fakta paling penting untuk diingat di sini adalah bahwa gerakan sepanjang sumbu tegak lurus adalah independen dan dengan demikian dapat dianalisis secara terpisah. Dimana gerakan vertikal dan horizontal terlihat independen. Kunci untuk menganalisis gerakan Parabola dua dimensi adalah dengan memecahnya menjadi dua gerakan, satu di sepanjang sumbu horizontal dan yang lainnya di sepanjang vertikal. (Pilihan sumbu ini adalah yang paling masuk akal, karena percepatan gravitasi adalah vertikal—sehingga, tidak akan ada percepatan sepanjang sumbu horizontal ketika hambatan udara diabaikan.) Seperti biasa, kita menyebut sumbu horizontal sebagai sumbu x dan sumbu vertikal sumbu y. Gambar 1 mengilustrasikan notasi perpindahan, di mana s didefinisikan sebagai perpindahan total dan x dan y masing-masing adalah komponennya sepanjang sumbu horizontal dan vertikal. Besaran vektor-vektor tersebut adalah s, x, dan y.
Gerak Parabola adalah suatu bentuk gerak yang dialami oleh suatu benda atau partikel (Proyektil) yang diproyeksikan di dekat permukaan bumi dan bergerak sepanjang jalur melengkung di bawah aksi gravitasi saja (khususnya, efek hambatan udara bersifat pasif dan diasumsikan diabaikan). Jalur melengkung ini ditunjukkan oleh Galileo sebagai parabola, tetapi mungkin juga berupa garis dalam kasus khusus ketika dilemparkan langsung ke atas. Studi tentang gerakan semacam itu disebut balistik, dan lintasan seperti itu adalah lintasan balistik. Satu-satunya kekuatan signifikansi matematis yang secara aktif diberikan pada objek adalah gravitasi, yang bertindak ke bawah, sehingga memberikan objek percepatan ke bawah menuju pusat massa bumi. Karena kelembaman benda, tidak diperlukan gaya luar untuk mempertahankan komponen kecepatan horizontal dari gerak benda. Mempertimbangkan kekuatan lain, seperti hambatan aerodinamis atau propulsi internal (seperti dalam roket), memerlukan analisis tambahan. Rudal balistik adalah peluru kendali yang hanya dipandu selama fase penerbangan bertenaga awal yang relatif singkat, dan arah yang tersisa diatur oleh hukum mekanika klasik.
Balistik (Yunani: βάλλειν, diromanisasi: ba'llein, lit. 'melempar') adalah ilmu tentang dinamika yang berhubungan dengan penerbangan, perilaku dan efek Parabola, terutama peluru, bom terarah, roket, atau sejenisnya; ilmu atau seni merancang dan mempercepat Parabola untuk mencapai kinerja yang diinginkan.
Lintasan Parabola dengan hambatan udara dan kecepatan awal yang bervariasi
Persamaan dasar balistik mengabaikan hampir setiap faktor kecuali kecepatan awal dan percepatan gravitasi konstan yang diasumsikan. Solusi praktis dari masalah balistik sering memerlukan pertimbangan hambatan udara, angin silang, gerakan target, berbagai percepatan gravitasi, dan dalam masalah seperti peluncuran roket dari satu titik di Bumi ke titik lain, rotasi Bumi. Solusi matematika terperinci dari masalah praktis biasanya tidak memiliki solusi bentuk tertutup, dan oleh karena itu memerlukan metode numerik untuk mengatasinya.
Apa itu Proyektil?
Proyektil adalah benda apa pun yang dilemparkan ke ruang angkasa di mana satu-satunya gaya yang bekerja adalah gravitasi. Gaya utama yang bekerja pada Proyektil adalah gravitasi. Ini tidak berarti bahwa kekuatan lain tidak bekerja padanya, hanya saja efeknya minimal dibandingkan dengan gravitasi. Jalur yang diikuti oleh Proyektil dikenal sebagai lintasan. Bola bisbol yang dipukul atau dilempar adalah contoh Proyektil.
Apa itu Gerak Parabola?
Ketika sebuah partikel dilemparkan miring di dekat permukaan bumi, ia bergerak sepanjang jalur melengkung di bawah percepatan konstan yang diarahkan ke pusat bumi (kita asumsikan bahwa partikel itu tetap dekat dengan permukaan bumi). Lintasan partikel semacam itu disebut Parabola dan geraknya disebut gerak parabola.
- Sebuah gelas tidak sengaja jatuh dari meja.
- Sebuah telepon dilemparkan ke tempat tidur.
- Sebuah rudal dikerahkan dari pesawat militer dari penerbangan tingkat.
- Lembing yang dilempar oleh seorang atlet.
Asumsi Gerak Parabola
- Tidak ada gesekan karena udara.
- Efek karena kelengkungan bumi dapat diabaikan.
- Efek akibat rotasi bumi dapat diabaikan.
- Seluruh lintasan berada di dekat permukaan bumi.
Kecepatan dan Percepatan dalam Gerak Parabola
Kecepatan parabola berubah. secara tangensial terhadap lintasan. Saat lintasan melengkung, kecepatan juga berubah arah.
Prinsip Kemandirian Fisik Gerak
- Gerak Parabola merupakan gerak dua dimensi. Jadi, dapat dibahas dalam dua bagian: gerak horizontal dan gerak vertikal. Kedua gerakan ini terjadi secara independen satu sama lain. Ini disebut prinsip kemandirian fisik gerakan.
- Kecepatan parabola dapat dibagi menjadi dua komponen yang saling tegak lurus: komponen horizontal dan komponen vertikal.
- Percepatan mengubah kecepatan. Jika percepatan dalam arah tertentu adalah nol, maka kecepatan dalam arah itu tetap sama. Jadi, dalam gerakan parabola, komponen kecepatan horizontal tetap tidak berubah selama penerbangan. Gerak mendatar merupakan gerak beraturan.
- Gaya gravitasi terus menerus mempengaruhi komponen vertikal, sehingga gerak vertikal merupakan gerak dipercepat beraturan.
- Proyektil dapat dilempar dengan berbagai cara: di tanah datar, dari menara tinggi ke tanah, dari pesawat terbang, dll. Bagian berikut membahas beberapa kasus secara rinci.
Gerakan Parabola
Proyektil adalah benda apa pun yang dilemparkan ke luar angkasa dengan hanya gravitasi yang bekerja padanya. Gaya utama yang bekerja pada proyektil adalah gravitasi. Ini bukan untuk mengatakan bahwa kekuatan lain tidak bertindak di atasnya; sebaliknya, dampaknya minimal jika dibandingkan dengan gravitasi. Lintasan adalah lintasan yang ditempuh secara parabola.
Ketika sebuah partikel dilemparkan secara miring di dekat permukaan bumi, ia mengikuti jalur melengkung dengan percepatan konstan menuju pusat bumi (kita asumsikan bahwa partikel itu tetap dekat dengan permukaan bumi). Lintasan partikel semacam itu dikenal sebagai lintasan parabola, dan gerakannya dikenal sebagai gerak parabola.
Gerak parabola juga adalah salah satu jenis gerak yang paling umum di pesawat. Satu-satunya percepatan yang bekerja dalam gerak peluru adalah percepatan vertikal yang disebabkan oleh gravitasi (g). Akibatnya, persamaan gerak dapat digunakan secara terpisah pada sumbu X dan Y untuk menentukan parameter yang tidak diketahui.
Gerak parabola dalam dua dimensi dibagi menjadi dua bagian:
- Gerak horizontal dalam arah x tanpa percepatan dan
- Gerak vertikal dalam arah y dengan percepatan konstan karena gravitasi.
Persamaan gerak parabola adalah y = ax + bx^2.
Untuk menyederhanakan perhitungan, gerakan parabola biasanya dihitung tanpa memperhitungkan hambatan udara.
Sebelum memahami turunan hubungan gerak parabola, mari kita kenalkan dulu beberapa istilah yang digunakan di dalamnya, yaitu:
- Sudut Proyeksi: Sudut di mana tubuh diproyeksikan terhadap horizontal disebut sebagai sudut proyeksi.
- Kecepatan Proyeksi: Kecepatan dengan mana tubuh dilemparkan disebut sebagai kecepatan proyeksi.
- Titik Proyeksi: Titik proyeksi adalah titik dari mana tubuh diproyeksikan di udara.
- Lintasan Parabola: Jalur yang diambil oleh proyektil di udara disebut sebagai lintasan parabola.
- Jangkauan Horizontal: Jarak horizontal yang ditempuh oleh tubuh yang melakukan gerakan parabola disebut sebagai jangkauan parabola.
Berikut ini kami berikan beberapa contoh soal beserta pembahasannya untuk membantu siswa memahami materi gerak parabola.
Tag:
gerak parabola
contoh gerak parabola
rangkuman gerak parabola
materi gerak parabola pdf
contoh soal gerak parabola
analisis vektor pada gerak parabola
rumus gerak parabola
tujuan gerak parabola
contoh soal gerak parabola beserta jawabannya
contoh soal gerak parabola dalam kehidupan sehari hari
soal gerak parabola pilihan ganda
soal dan pembahasan gerak parabola pdf
soal gerak parabola doc
contoh soal gerak parabola kelas 10 beserta jawabannya
contoh soal gerak parabola
contoh soal gerak parabola mencari sudut elevasi
Pelajaran Matematika Bentuk Aljabar
Kata aljabar berasal dari bahasa Arab: الجبر, diromanisasi: al-jabr,dari judul buku awal abad ke-9 Ilm al-jabr wa l-muqābala, "The Science of Restoring and Balancing" oleh ahli matematika dan astronom Persia al-Khwarizmi. Dalam karyanya, istilah al-jabr mengacu pada operasi memindahkan istilah dari satu sisi persamaan ke sisi lain, المقابلة al-muqābala "menyeimbangkan" mengacu pada penambahan istilah yang sama ke kedua sisi. Dipendekkan menjadi hanya aljabar atau aljabar dalam bahasa Latin, kata itu akhirnya memasuki bahasa Inggris selama abad ke-15, dari bahasa Spanyol, Italia, atau Latin Abad Pertengahan. Ini awalnya mengacu pada prosedur bedah pengaturan tulang yang patah atau terkilir. Makna matematis pertama kali dicatat (dalam bahasa Inggris) pada abad ke-16.
Ekspresi aljabar adalah ekspresi yang dibangun dari konstanta bilangan bulat, variabel, dan operasi aljabar (penambahan, pengurangan, perkalian, pembagian dan eksponen dengan eksponen yang merupakan bilangan rasional). Misalnya, 3x^2 2xy + c adalah ekspresi aljabar.
Sebaliknya, bilangan transendental seperti dan e bukan aljabar, karena tidak diturunkan dari konstanta bilangan bulat dan operasi aljabar. Biasanya, dibangun sebagai hubungan geometris, dan definisi e membutuhkan jumlah operasi aljabar yang tak terbatas.
Ekspresi rasional adalah ekspresi yang dapat ditulis ulang menjadi pecahan rasional dengan menggunakan sifat-sifat operasi aritmatika (sifat komutatif dan sifat asosiatif penjumlahan dan perkalian, sifat distributif dan aturan operasi pada pecahan). Dengan kata lain, ekspresi rasional adalah ekspresi yang dapat dibangun dari variabel dan konstanta dengan hanya menggunakan empat operasi aritmatika.
Polinomial homogen (kata lain dari bentuk aljabar), kadang-kadang disebut quantic dalam teks-teks yang lebih tua, adalah polinomial yang semua suku bukan nol memiliki derajat yang sama..
Bentuk aljabar, atau bentuk sederhana, adalah fungsi yang didefinisikan oleh polinomial homogen. Bentuk biner adalah bentuk dalam dua variabel. Bentuk juga merupakan fungsi yang didefinisikan pada ruang vektor, yang dapat dinyatakan sebagai fungsi homogen dari koordinat atas basis apa pun.
Sebuah polinomial derajat 0 selalu homogen; itu hanyalah elemen medan atau cincin koefisien, biasanya disebut konstanta atau skalar. Bentuk derajat 1 adalah bentuk linier.Bentuk derajat 2 adalah bentuk kuadrat. Dalam geometri, jarak Euclidean adalah akar kuadrat dari bentuk kuadrat.
Polinomial homogen ada di mana-mana dalam matematika dan fisika. Mereka memainkan peran mendasar dalam geometri aljabar, sebagai berbagai aljabar proyektif didefinisikan sebagai himpunan nol umum dari satu set polinomial homogen.
Polinomial homogen adalah polinomial multivariat (yaitu polinomial lebih dari satu variabel), dengan semua suku derajat yang sama. Cara lain untuk menyatakan ini: polinomial homogen derajat d jika merupakan kombinasi linier dari monomial derajat d.
Polinomial homogen umum kadang-kadang disebut bentuk aljabar:
Derajat 1 adalah bentuk linier,
Derajat 2 adalah bentuk kuadrat,
Derajat 3 adalah bentuk kubik.
Polinomial homogen berderajat k juga merupakan fungsi homogen berderajat k. Namun, kebalikannya tidak benar: ada banyak fungsi homogen yang bukan polinomial.
Untuk pemahaman selanjutnya, mari kita bedah bersama-sama soal dan pembahasannya
Tag:
contoh soal bentuk aljabar
bentuk aljabar kelas 7
bentuk aljabar
penjumlahan bentuk aljabar
perkalian bentuk aljabar
rumus bentuk aljabar
operasi penjumlahan dan pengurangan bentuk aljabar dapat disederhanakan apabila
contoh bentuk aljabar 3 suku
Pelajaran Matematika Grafik Fungsi Kuadrat
Fungsi kuadrat yaitu fungsi yang persamaannya memiliki variabel dengan pangkat tertingginya 2. Dalam materi fungsi kuadrat kita pelajari ciri-ciri grafik fungsi kuadrat,sumbu simetri, nilai optimum (maksimum atau minimum) serta titik potongnyaterhadap sumbu pada koordinat kartesius.
Persamaan umumfungsi kuadrat adalah :
F(x)=ax2 + bx + c atau y=ax2 + bx + c
Variabel x padafungsi kuadrat adalah variabel bebas sedangkan y sebagai variabel terikat. adan b sebagai koefisien dimana a ≠ 0 danc sebagai konstanta.
Grafik fungsi kuadrat adalah grafik berbentuk kurva parabola yangdihasilkan dari persamaan kuadrat yang digambarkan pada bidang kartesius.
Fungsi kuadrat
Fungsi kuadrat digunakan di berbagai bidang teknik dan sains untuk mendapatkan nilai parameter yang berbeda. Secara grafis, mereka diwakili oleh parabola. Bergantung pada koefisien derajat tertinggi, arah kurva ditentukan. Kata “Quadratic” berasal dari kata “Quad” yang berarti persegi. Dengan kata lain, fungsi kuadrat adalah "fungsi polinomial derajat 2." Ada banyak skenario di mana fungsi kuadrat digunakan. Tahukah Anda bahwa ketika sebuah roket diluncurkan, jalurnya dijelaskan oleh solusi fungsi kuadrat?
Fungsi kuadrat adalah fungsi polinomial dengan satu atau lebih variabel yang eksponen tertinggi variabelnya adalah dua. Karena suku derajat tertinggi dalam fungsi kuadrat adalah derajat kedua, maka disebut juga polinomial derajat 2. Sebuah fungsi kuadrat memiliki minimal satu suku derajat kedua.
Pada artikel ini, kita akan menjelajahi dunia fungsi kuadrat dalam matematika. Anda akan belajar tentang grafik fungsi kuadrat, rumus fungsi kuadrat, dan fakta menarik lainnya seputar topik ini.
Grafik fungsi kuadrat adalah parabola, dan bagian-bagiannya memberikan informasi yang berharga tentang fungsi tersebut.
Fitur Parabola
Parabola memiliki beberapa fitur yang dapat dikenali yang mencirikan bentuk dan penempatannya pada bidang Cartesian.
Puncak (vertex)
Salah satu fitur penting dari parabola adalah memiliki titik ekstrem, yang disebut titik. Jika parabola terbuka, simpul mewakili titik terendah pada grafik, atau nilai minimum fungsi kuadrat. Jika parabola terbuka ke bawah, simpul mewakili titik tertinggi pada grafik, atau nilai maksimum. Dalam kedua kasus, simpul adalah titik balik pada grafik.
Sumbu Simetri
Parabola juga memiliki sumbu simetri yang sejajar dengan sumbu y. Sumbu simetri adalah garis vertikal yang ditarik melalui titik sudut.
Perpotongan y
Perpotongan y adalah titik di mana parabola memotong sumbu y. Tidak boleh ada lebih dari satu titik seperti itu, untuk grafik fungsi kuadrat. Jika ada, kurva tidak akan menjadi fungsi, karena akan ada dua nilai y untuk satu nilai x, pada nol.
Perpotongan x
Perpotongan x adalah titik potong parabola terhadap sumbu x. Jika ada, perpotongan x mewakili nol, atau akar, dari fungsi kuadrat, nilai x di mana y=0. Mungkin ada nol, satu, atau dua perpotongan x. Jumlah perpotongan x bervariasi tergantung pada lokasi grafik.
Persamaan polinomial dengan pangkat tertinggi dari variabelnya adalah 2 disebut fungsi kuadrat. Kami tiba di grafik berikut ketika kami menggambar fungsi kuadrat seperti y = x^2:
Kita dapat dengan mudah melihat bahwa kita tidak berhadapan dengan garis lurus tetapi parabola, sehingga disebut sebagai fungsi non-linier. Ketika seseorang memiliki koefisien positif sebelum x2 kita memiliki nilai minimum, dan jika kita memiliki koefisien negatif, kita memiliki nilai maksimum sebagai gantinya. Lihat grafik di bawah ini di mana y = -x^2:
Aturan praktis mengingatkan kita bahwa ketika kita memiliki simbol positif sebelum x^2 kita mendapatkan ekspresi bahagia pada grafik :) dan simbol negatif membuat ekspresi sedih :(
Keterangan Pelajaran Selanjutnya dalam bentuk grafik dan rumus :
Tag:
contoh soal grafik fungsi kuadrat
contoh soal fungsi kuadrat dan grafik parabola
grafik fungsi kuadrat f
contoh soal grafik fungsi kuadrat
grafik fungsi kuadrat kelas 9
contoh soal grafik fungsi kuadrat kelas 9
sifat grafik fungsi kuadrat
kesimpulan grafik fungsi kuadrat
Pelajaran Luas Bangun Datar Gabungan Lingkaran