Berikut ini Bimbel Jakarta Timur memberikan SOAL PAT MATEMATIKA KELAS 8 untuk menghadapi Ujian kenaikan Kelas (UKK) untuk kelas 8. PAT Matematika
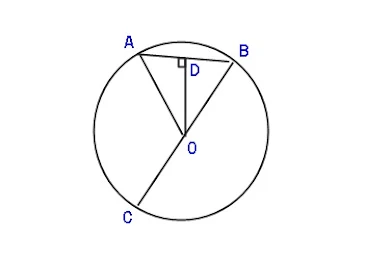
1. Perhatikan gambar berikut !
Garis AB disebut...
A. Jari-jari
B. Busur
C. Tali busur
D. Apotema
2. Panjang jari-jari sebuah lingkaran adalah 14 cm. Keliling lingkaran tersebut dengan p = 22/7 adalah...
A. 44 cm C. 88 cm
B. 66 cm D. 176 cm
3. Luas suatu lingkaran 38,5 cm². Jika p=22/7, maka keliling lingkaran tersebut adalah...
A. 44 cm C. 11 cm
B. 22 cm D. 7 cm
4. Hitung luas juring lingkaran yang bersudut 36° dan berjari-jari 20 cm !
A. 1256 cm² C. 628 cm²
B. 125,6 cm² D. 62,8 cm²
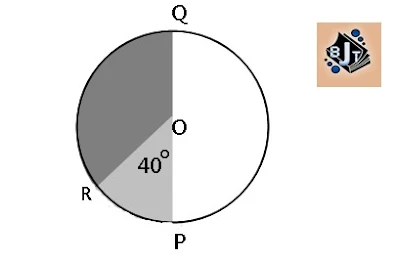
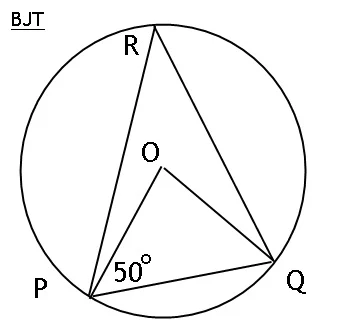
5. Pada gambar di bawah <POR=40° dan luas OPR=120 cm².
Luas juring OQR=....
A. 70 cm²
B. 140 cm²
C. 210 cm²
D. 420 cm²
6. Pada gambar dibawah <AOB=40° dan <BOC=50°.
Jika panjang busur AB=24 cm, maka panjang busur BC adalah....
A. 25 cm
B. 30 cm
C. 35 cm
D. 40 cm
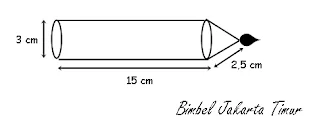
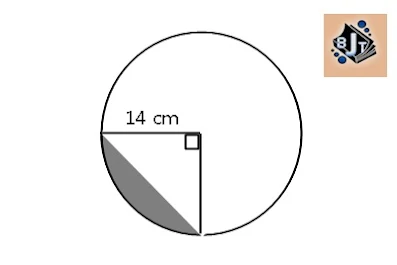
7. Luas tembereng pada gambar di bawah adalah...
A. 56 cm²
B. 98 cm²
C. 112 cm²
D. 154 cm²
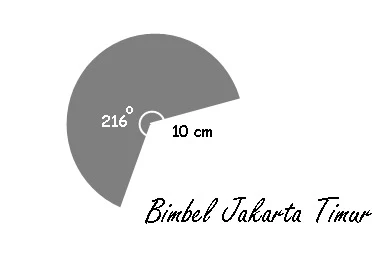
8. Luas daerah arsiran di bawah adalah...
A. 308 cm²
B. 616 cm²
C. 924 cm²
D. 1.232 cm²
9. Roda sepeda berjari-jari 35 cm dan berputar sebanyak 2.000 kali. Panjang lintasan yang dilalui sepeda tersebut adalah …. (p = 22/7)
A. 0,7 km C. 4,4 km
B. 44 km D. 70 km
10. . Suatu taman berbentuk lingkaran dengan jari-jari 28 m. Di dalam taman dibuat kolam yang berbentuk lingkaran dengan diameter 40 m. Di luar kolam di dalam taman ditanami rumput.
Bila harga rumput dan biaya pemasangan Rp10.000,00 tiap m2,biaya yang diperlukan seluruhnya adalah ….
A. Rp12.200.000,00 C. Rp12.080.000,00
B. Rp5.600.000,00 D. Rp 1.860.000,00
11. Pada gambar di bawah, panjang AB = 6 cm, BC = 15 cm dan <BCD=60°.
Keliling bangun yang diarsir adalah...
A. 18,84 cm
B. 37,68 cm
C. 30,84 cm
D. 49,68 cm
12. Tentukan besar <POQ pada gambar di bawah ini !
A. 90o
B. 135o
C. 45o
D. 22,5o
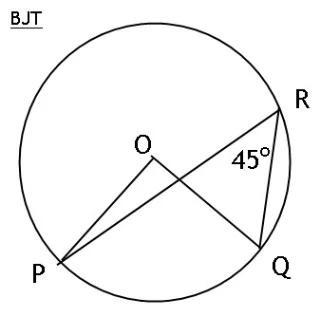
13.Tentukan besar <PRQ pada gambar di bawah ini!
A. 20o
B. 30o
C. 40o
D. 50o
14. Jika PR adalah diameter lingkaran, maka besar<PRQ adalah…
A. 18o
B. 36o
C. 54o
D. 72o
15. Jika panjang jari-jari lingkaran pada gambar di samping adalah 15 cm dan panjang garis singgung QR 20 cm, maka panjang garis PR adalah…
A. 18 cm
B. 24 cm
C. 30 cm
D. 32 cm
16. Dua buah lingkaran memiliki panjang jari-jari 10 cm dan 5 cm.Jika jarakkedua pusat lingkaran adalah 25 cm, maka panjang garis singgungpersekutuan dalam adalah..
A. 10 cm C. 24 cm
b. 20 cm D. 30 cm
17. Duabuah lingkaran dengan jarak pusatnya 34 cm dan panjang garis singgung lingkaranluar 30 cm. Jika panjang jari-jari salah satu lingkaran adalah 20 cm, maka panjangjari-jari lingkaran yang lain adalah…
A. 12 cm C. 6 cm
B. 8 cm D. 4 cm
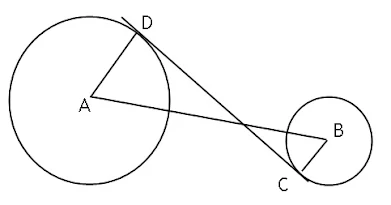
18. Pada gambar di bawah ini, CD adalah garissinggung persekutuan dalam dari dua lingkaran yang berpusat di A dan B.
Jika jarak AB=29 cm, CD=21 cmdan panjang jari-jari A dan panjang jari-jari B berbanding 3 : 2, tentukanpanjang jari-jari A dan B!
A. 18 cm dan 12 cm
B. 15 cm dan 10 cm
C. 12 cm dan 8 cm
D. 9 cm dan 6 cm
19. Sebuah segitiga panjang sisinya 15 cm, 20 cm dan 25 cm. Berapa panjang jari-jari lingkaran dalam segitiga tersebut !
A. 2,5 cm C. 5 cm
B. 3 cm D. 6 cm
20.Tentukan panjang jari-jari lingkaran luar dari segitiga yang panjang sisinya 10 cm, 17 cm dan 21 cm !
A. 10,125 cm C. 10,5 cm
B. 10,25 cm D. 10,625 cm
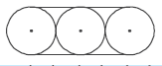
21.Gambar di bawah adalah penampang tiga buah pipa air yang berbentuk tabung dengan diameter 14 cm.
Berapakah panjang tali minimaluntuk mengikat tiga buah pipa dengan susunan tersebut?
A. 112 cm C. 84 cm
B. 100 cm D. 56 cm
22. Bangun ruang yang memiliki 9 rusuk dan 5 sisi adalah...
A. persegi C. limas segiempat
B. prisma trapesium D. prisma segitiga
23. Suatu kubus memiliki panjang diagonal ruang 8v3 cm. Berapakah volume kubus tersebut?
A. 512 cm³ C. 1.536 cm³
B. 1.024 cm³ D. 1.600 cm³
24, Sebuah balok memiliki ukuran 12 cm x 4 cm x 3 cm. panjang diagonal ruangnya adalah....
A. 15 cm C. 13 cm
B. 14 cm D. 12,5 cm
25. Sebuah balok berukuran panjang=20 cm,lebar=12 cm dan tinggi 9 cm. Tentukan luas permukaan balok tersebut !
A. 2.160 cm² C. 1.008 cm²
B. 1.800 cm² D. 1.056 cm²
26. Sebuah balok mempunyai luas alas 240 cm2, sisi depan 180 cm2 dan sisi samping 108 cm2. Volum balok tersebut adalah...
A. 2.160 cm³ C. 1.008 cm³
B. 1.800 cm³ D. 1.056 cm³
27. Sebuah prisma segitiga yang ukuran sisi alasnya 6 cm, 8 cm, 10 cm dan tinggi prisma 15 cm. Tentukan luas permukaan prisma tersebut !
A. 360 cm² C. 408 cm²
C. 384 cm² D. 432 cm²
28. Sebuah prisma segitigaABC.DEF dengan panjang AB=BC=17 cm dan AC=16 cm. Jika tinggi prismaadalah 25 cm, tentukan volume prisma tersebut !
A. 2.160 cm³ C. 3.000 cm³
B. 2.800 cm³ D. 3.056 cm³
29. Sebuah balok berukuran panjang (2x+6) cm, lebar (2x-2) cm dan tinggi (3x+4) cm. Sedangkan jumlah panjang rusuk-rusuknya 228 cm. Hitunglah tinggi balok tersebut !
A. 12 cm C. 20 cm
B. 14 cm D. 25 cm
30. Sebuah bak berbentuk kubus volumenya 512 liter berisi penuhair. Jika Aldi mandi menggunakan air sebanyak 128 liter, maka ketinggian airsekarang adalah…
A. 12 cm C. 20 cm
B. 14 cm D. 25 cm
31. Luas permukaan limas yang alasnya berbentuk persegi dengan panjang sisi 12 cm dan tinggi limas 8 cm adalah....
A. 384 cm2 C. 480cm2
B. 428 cm2 D. 768 cm2
32. Budi mempunyai kawat sepanjang 24 meter. Ia akan membuatkerangka balok yang berukuran 15 cm x 12cm x 13 cm. Banyak kerangka balok yang dapat dibuat adalah ….
A. 10 buah C. 13buah
B. 12 buah D. 15 buah
33. Sebuah kolam renang bagian dangkalnya sedalam 1 m dan melandai sampai kedalaman 2,5 m. Jika permukaan kolam renang bagian atas berukuran 15 m x 20 m, berapa volume air yang dibutuhkan untuk mengisi kolam renang tersebut sampai penuh?
A. 1.050 cm³ C. 525 cm³
B. 1.025 cm³ D. 456 cm³
34. Sebuah limas memiliki alas ebrbentuk persegi dengan luas 144 cm². Jika panjang rusuk tegak limas adalah 13 cm, maka luas limas persegi tersebut adalah...
A. 364 cm2 C. 400 cm2
B. 384 cm2 D. 468 cm2
35. Sebuah limas yang alasnya persegi panjang berukuran 24 cmx 18 cm. Jika rusuk tegak limas adalah 25 cm, maka volume limas tersebut adalah...
A. 1.024 cm³ C. 4.320 cm³
B. 2.160 cm³ D. 6.480 cm³
Demikian kumpulan soal latihan yang dapat kami berikan. Semoga dapat membantu dalam mempersiapkan diri untuk UKK sekolah anda.
Baca Juga
https://www.radarhot.com/2018/05/latihan-ukkpat-matematika-kelas-8.html